1. 贝塞尔曲线
2. 二次贝塞尔曲线
2.1 命令Q
| 命令 | 名称 | 参数 |
|---|---|---|
| Q | quadratic Bezier curveto | (x1,y1 x,y) |
2.2 表达式
2.3 切线表达式
2.4 示例
2.5 源码
<svg xmlns="http://www.w3.org/2000/svg" width="740" height="300">
<path d="M10 10 Q350,480 700,10" stroke="red" fill="transparent"/>
</svg>
1
2
3
2
3
3. 二次贝塞尔曲线T命令
3.1 命令T
| 命令 | 名称 | 参数 |
|---|---|---|
| T | smooth quadratic Bezier curveto | (x,y) |
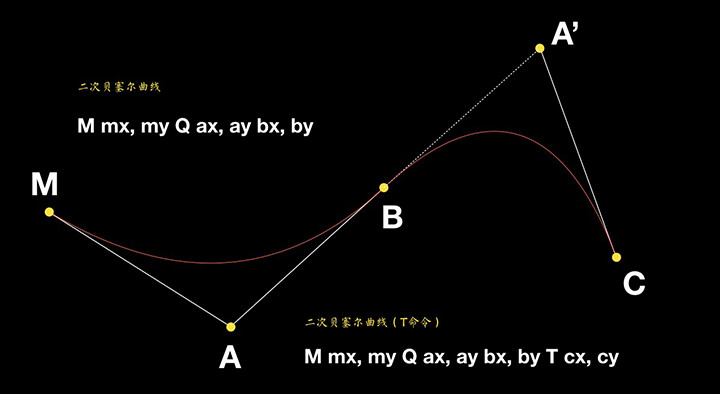
"快捷命令T会通过前一个控制点,推断出一个新的控制点。这意味着,在你的第一个控制点后面,可以只定义终点",图示解释:T命令会以B为对称点,得出A点的镜像A',我们只需要确定终点C,即可得到由B、A'、C作为控制点的二次贝塞尔曲线;我们可以继续添加T命令,绘制出更多的二次贝塞尔曲线,这些曲线首尾光滑连接。T命令前面必须是一个Q命令,或者是另一个T命令,如下图所示:
3.2 示例
3.3 源码
<svg xmlns="http://www.w3.org/2000/svg" width="720" height="300">
<path d="M18 160 Q230,330 450,150 T754,366" stroke="red" fill="transparent"/>
</svg>
1
2
3
2
3
4. 三次贝塞尔曲线
4.1 命令C
| 命令 | 名称 | 参数 |
|---|---|---|
| C | curveto | (x1,y1 x2,y2 x,y) |
4.2 表达式
4.3 示例
4.4 源码
<svg xmlns="http://www.w3.org/2000/svg" width="720" height="300">
<path d="M10 10 C250,480 400,-100 700,90" stroke="red" fill="transparent"/>
</svg>
1
2
3
2
3
5. 三次贝塞尔曲线S命令
5.1 命令S
| 命令 | 名称 | 参数 |
|---|---|---|
| S | smooth curve | (x2,y2 x,y) |
5.2 示例
S命令要分两种情况:
- 情况一:S命令跟在一个C命令或者另一个S命令的后面: 此种情况的S命令同T命令原理相同,它的前两个控制点不需要提供(由对称镜像所得),只需要提供后面两个控制点坐标即可
- 源码
<svg xmlns="http://www.w3.org/2000/svg" width="720" height="300">
<path d="M30,208 C65,47 154,47 194,103 S320,395 506,57" stroke="red" fill="transparent"/>
</svg>
1
2
3
2
3
- 情况二:S命令单独使用: "前面没有C命令或者另一个S命令,那么它的两个控制点就会被假设为同一个点" —— 这句话摘自MDN,“两个控制点假设为同一个点”实在不理解,实验发现,此时S命令与Q命令达到效果一致,均为二次贝塞尔曲线。下面示例与示例2.4效果一致。
- 源码
<svg xmlns="http://www.w3.org/2000/svg" width="720" height="300">
<path d="M10 10 S350,480 700,10" stroke="red" fill="transparent"/>
</svg>
1
2
3
2
3
6 命令汇总
| 命令 | 名称 | 参数 |
|---|---|---|
| Q | quadratic Bezier curveto | (x1,y1 x,y) |
| T | smooth quadratic Bezier curveto | (x,y) |
| C | curveto | (x1,y1 x2,y2 x,y) |
| S | smooth curve | (x2,y2 x,y) |


